Si no has leído la primera entrada de esta saga, entra aquí:
Ahora que ya sabemos orientarnos y movernos por el espacio-tiempo, cabe preguntarse cómo se vive dentro. ¿Ven lo mismo y a la misma vez todos los observadores?
Vamos a hacer un pequeño experimento mental. Imaginemos que Pepe está en una nave espacial viajando dentro de su cono de luz cuando, de repente, María le adelanta con otra nave a una cierta velocidad V (que se calcula como V=tg(v) ). Pepe será el observador O, y María el observador O’. Ésto se representaría de la siguiente forma
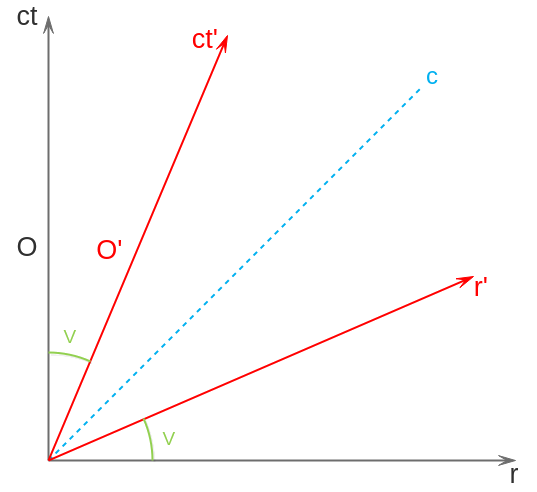
Como la velocidad de la luz (c) es constante y la misma tanto para uno como para otro, y dado que María lleva una velocidad V respecto de Pepe, los ejes de coordenadas para María deben ser simétricos con c y a su vez tener un ángulo v respecto a los de Pepe.
Ahora imaginemos que ambos observadores ven ocurrir dos eventos (a y b). ¿Cómo los ven?
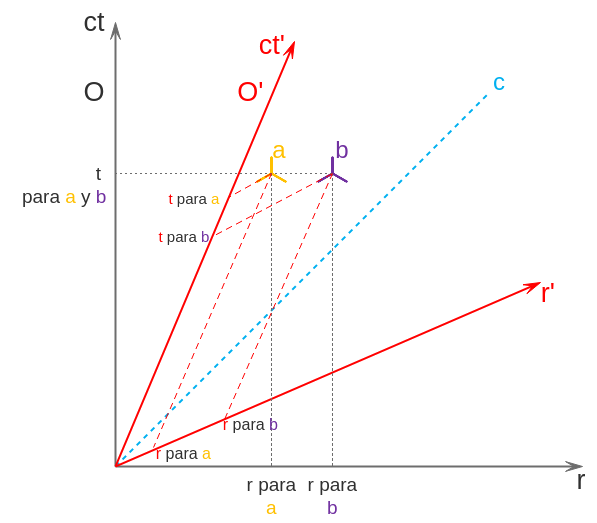
Como veis, para Pepe ambos eventos ocurren en el mismo tiempo, es decir, son simultáneos. Sin embargo, para María no lo son, ocurren en dos tiempos diferentes. Los eventos son los mismos, pero las coordenadas tanto temporales como espaciales no son las mismas para ambos.
La física es la misma, pero el camino por el que el llegamos a las conclusiones no tiene por qué serlo
Pongamos un ejemplo para que se entienda mejor: si suelto una pelota desde un tercer piso, la veré caer y diré que la pelota es atraída gravitacionalmente por la Tierra. Si Spiderman está colgando boca abajo en el edificio de enfrente observando, verá que la pelota flota hacia arriba, pero también concluirá que es porque la Tierra, que también la ve arriba, la atrae.
Con ésto ya hemos dejado patente que no todos los observadores ven lo mismo ni a la misma vez, sino que depende de su sistema de referencia, es decir, de las velocidades relativas entre ellos.
¿Significa esto que el espacio-tiempo es un mero escenario pasivo donde ocurren cosas y que nuestra percepción de esas cosas depende únicamente de cómo nos movemos por ese escenario? Pues no. Como diría el Dr. Frankenstein, ¡está vivo! Y es que el espacio-tiempo no es sólo escenario, sino que es también uno de los protagonistas e interactúa con todo aquello que contiene, por ejemplo, la masa.
Vamos ahora a utilizar una analogía muy manida, pero muy útil: si el espacio-tiempo fuera una tela estirada y tensa y nosotros colocásemos una manzana sobre ella; la tela se curvaría. Pues eso exactamente es lo que ocurre.
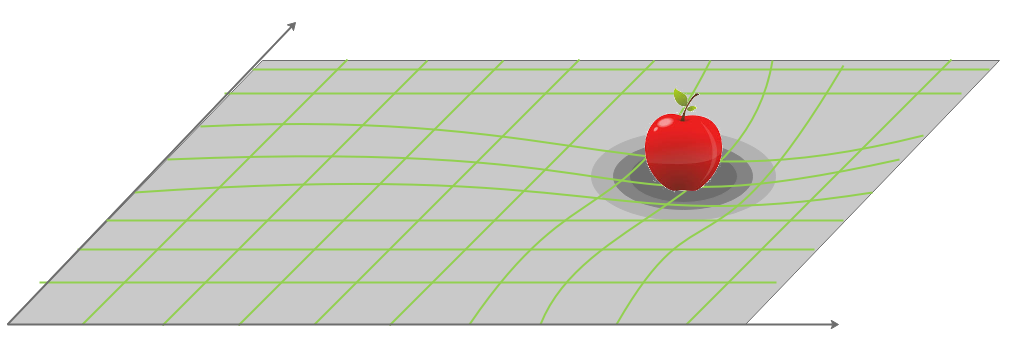
El espacio-tiempo está deformado por la materia y energía que contiene. La gracia es que nada puede salirse de la sábana, con lo cual estamos condenados a movernos por esas deformaciones.
Veamos algunos ejemplos y consecuencias de esto.
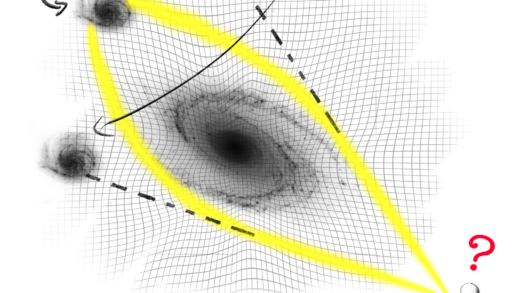
Lentes gravitacionales
Como se puede ver, si miramos hacia un objeto masivo vemos que algunas estrellas del fondo están repetidos de forma simétrica. La explicación es que no son objetos que están realmente ahí, sino es un único objeto que se sitúa exactamente detrás de la estrella a la que miramos. La luz que proviene de la estrella que está detrás cae en la deformación y la trayectoria de la luz se curva porque el espacio es curvo y no tiene más remedio que viajar por él, haciendo que parezca que está en otro sito al salir de la deformación. En función de lo alineados que estemos con ésta deformación, veremos el objeto repetido varias veces o directamente formando un anillo.


Órbitas
Ya sabemos que los planetas del Sistema Sola orbitan alrededor del Sol por atracción gravitatoria. Así nos lo dijo Newton y nuestros profesores en el colegio. Además, sus órbitas son las que son porque se han equilibrado en las que menos energía les requieren (todo en el universo tiende al estado de menor energía, que es el equilibrio).
Pero ahora sabemos que el Sol, mucho más masivo que los planetas, tiene necesariamente que deformar el espacio-tiempo.
Si dibujáis una línea recta en un globo terráqueo entre Madrid y Los Ángeles (verde), si luego pudierais ‘aplanar’ ese globo terráqueo para convertirlo en un mapa en papel, veríais que vuestra línea recta no es tal.
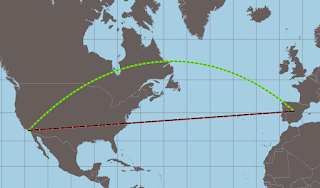
Las líneas rectas en espacios curvos son curvas en espacios planos
¿Y si ahora os decimos que los planetas están siguiendo las trayectorias rectas menos energéticas en el espacio curvo debido a la deformación que el Sol provoca en el espacio-tiempo?
Tomaos un momento para comprender bien esto, porque acabamos de convertir la gravedad en algo opcional.
En efecto, la gravedad ahora es una fuerza que nos hemos inventado para poder explicar los movimientos de los planetas desde un sistema de referencia en el que el espacio es plano. Necesitamos la intervención de una fuerza para explicar por qué giran. Si asumimos que es curvo, el movimiento se explica solo, ya no nos hace falta ninguna fuerza. Es lo mismo que pasa con la fuerza centrífuga, que es necesaria si estamos montados en el tiovivo que gira e innecesaria si estamos fuera en reposo respecto del tiovivo.
¿Quiere decir ésto que Newton estaba equivocado? No necesariamente. Newton estaba estudiando el movimiento de los astros desde un sistema de referencia en el que no podía ver que el espacio-tiempo estaba deformado. Como hemos dicho al principio, la física es la misma, sus resultados sobre las órbitas y masas son correctos, aunque el camino para llegar a ellos ha sido diferente del nuestro hoy aquí.
2 Responses
[…] El escenario espacio-temporal (Minkowskii II) […]
[…] El escenario espacio-temporal (Minkowskii II) […]