Ya sabes que todo ocurre en un momento y lugar determinados. Lo que puede que no te hayas parado a pensar es que algo tan obvio a veces no es tan fácil de expresar de forma matemática. Por suerte, tenemos la ayuda de Hermann Minkowski (1864-1909).
El matemático, nacido en lo que hoy es Kaunas (Lituania), cursó sus estudios en Alemania y posteriormente fue profesor de un joven Albert Einstein en Zúrich. En 1907 se percató de que todo el aparatejo matemático que había tras la Relatividad Especial podía entenderse más fácilmente si expresamos precisamente la idea de que todo tiene un momento y un lugar, de forma matemática.
Normalmente para decir dónde se encuentra algo usamos coordenadas. Seguramente te suene de algo las palabras latitud y longitud, o hayas pasado alguna vez una ubicación de Google Maps y hayas visto esos números que indican las coordenadas. O quizás alguna vez hayas buscado un tesoro. En cualquier caso, hay muchos sistemas de coordenadas posibles, de manera que para decir donde se encuentra algo en un plano (es decir, dos dimensiones), nos basta con dos coordenadas que llamaremos x,y
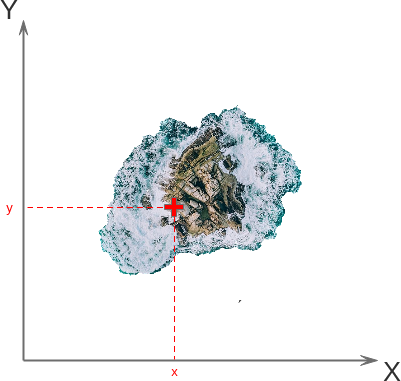
Sin embargo, si queremos decir dónde se encuentra algo en un volumen, en un espacio (es decir, tres dimensiones), ya necesitamos tres coordenadas, que aquí llamaremos x,y,z
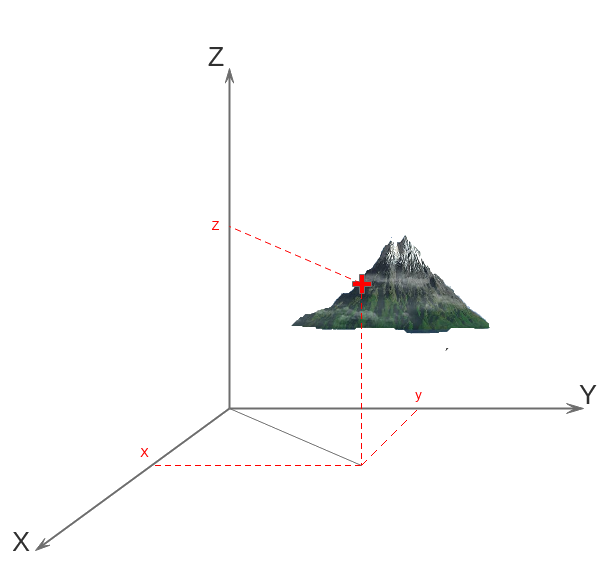
Ésto es lo que se llama sistema de coordenadas cartesianas.
Ahora que tenemos perfectamente definido dónde se encuentra algo, nos queda definir cuándo ocurre, es decir, nos hace falta una coordenada más para el tiempo. De ésta forma se define lo que llamamos un Evento, que queda perfectamente definido si conocemos sus tres coordenadas espaciales y su coordenada temporal
Evento= E(x,y,z,t)
Como ves, ahora nos movemos en cuatro dimensiones. Este espacio matemático de eventos es un espacio tetradimensional en el que el espacio y el tiempo están íntimamente relacionados, y es lo que conocemos como Espacio de Minkowski o Espacio-tiempo, y es precisamente el espacio en el que vivimos. Esta representación matemática de la realidad ayudó a Einstein a desarrollar la Relatividad General, que fue uno de las grandes revoluciones científicas.
Ahora que tenemos definido el espacio en el que vivimos, vamos a llenarlo de luz. Lamentablemente, nuestra mente diseñada tridimensionalmente no puede imaginar un espacio de 4 dimensiones, así que a partir de ahora vamos a proyectar esas cuatro dimensiones en el plano de un folio, de manera que lo que en la primera gráfica era la coordenada x, ahora representará el espacio (r), es decir, la composición de las tres coordenadas espaciales x, y, z; y lo que antes era la coordenada y, ahora será la coordenada temporal t.
De ésta forma, podremos localizar un evento puntual, o un evento que perdura en el tiempo en el mismo lugar como por ejemplo, la existencia de un agujero negro, como podéis ver aquí
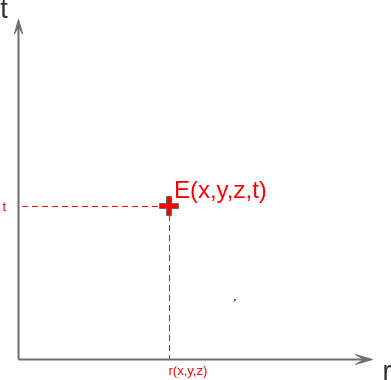
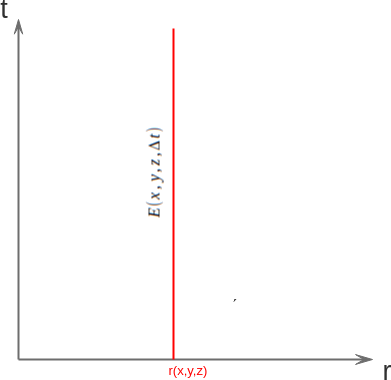
Para terminar, así se representa un evento que perdura en el tiempo y además se desplaza a cierta velocidad constante (izquierda) o a velocidad variable (derecha) de esta forma
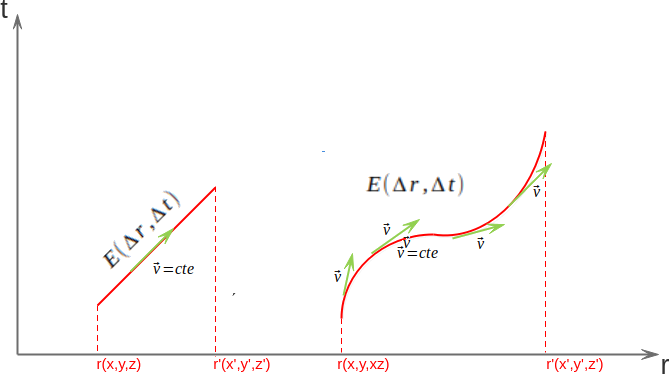
Además, podemos definir la velocidad como la pendiente de la tangente a la trayectoria, de manera que una línea con un ángulo menor con el eje r significa que recorre más espacio en menos tiempo, por lo que su velocidad es mayor; y una línea que forma un ángulo mayor con el eje r recorre menos espacio en el mismo tiempo, es decir, su velocidad es menor.
Entonces, si nos situamos en un lugar y tiempo determinados (en el vacío) y emitimos un pulso de luz, éste se desplazará a una velocidad constante de 300000Km/s que denotamos c, en todas direcciones y expandiéndose conforme avanza, lo que da lugar a un cono.
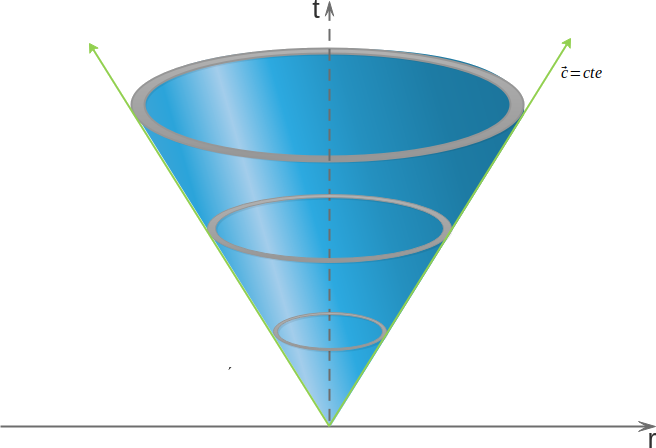
Es lo que llamamos un cono de luz. Ahora sumaremos que la Relatividad nos dice que c es una velocidad límite, nada con masa puede ir más rápido que la velocidad de la luz en el vacío. Esto significa que, como tenemos masa, no podemos ir más rápido que la luz, es decir, no podemos salirnos de nuestro cono.
Todos los futuros a los que podemos acceder se encuentran dentro de nuestro cono de luz
Vamos a situarnos ahora en el Universo. Imaginemos una malla infinita de conos de luz, ya que en todas partes pueden ocurrir eventos coetáneos. Por ejemplo podemos tener a dos personas (nuestros ya conocidos Pepe y María), que nacen en momentos y lugares diferentes
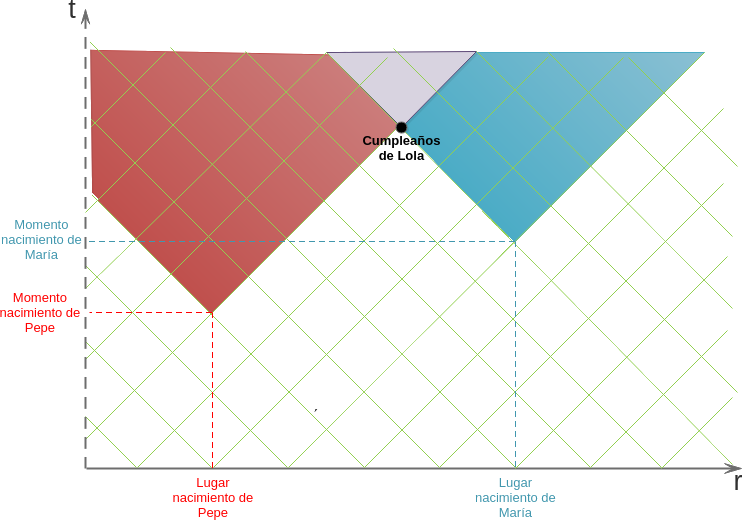
Cada uno de ellos tendrá su cono de luz, y no podrá salir de él porque no pueden viajar más rápido que la luz. Ni Pepe ni María pueden acceder a los posibles futuros que quedan fuera de sus respectivos conos, así que no pueden ejercer ninguna influencia en ellos, así que durante un tiempo no podrán conocerse. Sin embargo, hay un cierto tiempo a partir del cual sus conos de luz se solapan, lo que significa que hay futuros posibles a partir de ese tiempo en el que sí que pueden conocerse e influenciarse el uno al otro.
Pongamos que el evento exacto en el que sus conos se encuentran es el cumpleaños de su amiga en común, Lola. Si ambos van al cumpleaños, se conocerán justo en ese punto. Sin embargo, si María no va, sino que se queda en su lugar de nacimiento, ya no podrán conocerse en el cumpleaños de Lola, sino que tendrá que pasar un poco más de tiempo para que se solapen sus conos de luz y puedan conocerse.
Esto significa que hay futuros que nos están vetados y por tanto no podemos tener contacto causal con esos los eventos. Sin embargo, podemos pensar que sea lo que sea lo que hagan Pepe y María, si esperan el tiempo suficiente, en algún momento sus conos se solaparán y ellos podrán encontrarse. Aquí es donde entra en juego la expansión del Universo. Y es que el Universo se expande más rápido que la velocidad de la luz, lo que quiere decir que todo se aleja de todo tan rápido que hay lugares que nunca serán alcanzados por mi cono de luz, que nunca estarán en contacto causal. En todo el Universo ocurren eventos que nunca podrán conocerse en otros lugares determinados del mismo.

1 Response
[…] Luz, futuro y causalidad (Minkowskii I) […]