Si no has leído la anterior entrada de esta saga, entra aquí:
Ahora ya estamos preparados para hablar de singularidades. Una singularidad es un punto del espacio en el que el comportamiento de la física es extraño o simplemente nuestras ecuaciones no son evaluables en ese punto, por lo que no nos pueden dar información sobre lo que pasa en él. Por ejemplo, si tenemos la función
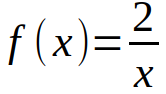
Si damos valores a la x, podemos saber cuanto vale en ese punto: si x=2, la función cale 1; si x=1, la función vale 0,5… Pero, ¿qué pasa si x=0? Pues como no se puede dividir por 0, no tenemos forma de saber cuánto vale la función en 0. Es decir, x=0 es una singularidad.
¿Existe algo parecido en el espacio-tiempo? ¿Hay singularidades en el espacio de Minkowski? Efectivamente, las hay, y podemos dividirlas en dos tipos:
- Singularidad de coordenadas: son simplemente un efecto del sistema de coordenadas que hemos elegido. Estas singularidades pueden evitarse simplemente eligiendo otro sistema de coordenadas. Por ejemplo:
Para calcular el potencial gravitatorio de una masa Q usamos la ecuación
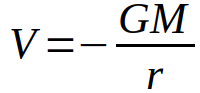
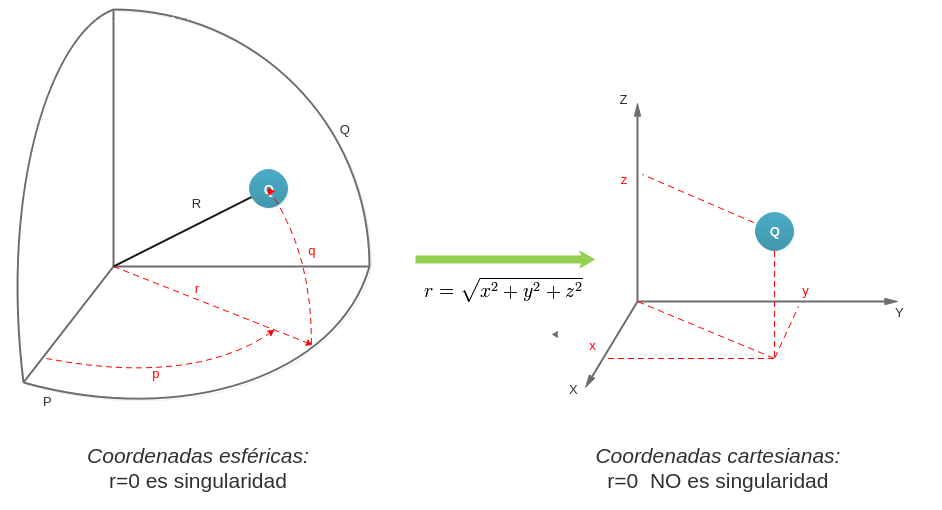
Si usamos las coordenadas esféricas y queremos calcularlo en el punto r=0 (distancia a la masa=0), igual que antes, como no se puede dividir por cero, tendremos una singularidad. Es decir, no podemos saber cuánto vale el potencial en ese punto. Sin embargo, si hacemos un cambio de coordenadas y pasamos a cartesianas, r ahora vale la raíz cuadrada de la suma de x, y, z al cuadrado, es decir, r ahora es diferente de 0 y por tanto ya podemos calcular el potencial.
Las singularidades de coordenadas pueden ‘esquivarse’ haciendo un cambio de sistema de coordenadas
- Singularidad física: es una singularidad real. En el espacio-tiempo, ésto se traduce como un agujero negro.
Recordemos que un agujero negro es el final de la vida de una estrella muy masiva. Cuando estas estrellas dejan de producir energía no hay nada que contrarreste el colapso y empiezan a comprimir toda su masa en un espacio cada vez más pequeño, es decir, aumentando mucho su densidad.
¿Cómo afecta ésto al espacio-tiempo? Recurriendo una vez más a la metáfora de la sábana, si nos lo imaginamos de perfil podemos ver como se ‘hunde’, se deforma, conforme avanza el colapso de la estrella moribunda.

Al mantenerse siempre su gran masa constante, pero reducirse su volumen, la densidad aumenta y la presión sobre el espacio-tiempo es cada vez mayor, haciendo la deformación cada vez más y más prominente. Veamos ahora cómo se representa ésto en el espacio de Minkowski. Para ello nos hará falta conocer las Ecuaciones de Einstein de la Relatividad General.
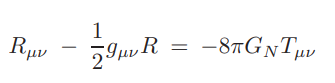
Esta ecuación fue el culmen del trabajo de Einstein en cuanto a la Relatividad. Son en realidad 10 ecuaciones que relacionan la geometría del espacio-tiempo con la energía y materia que contiene. Con ella, y sabiendo la masa y el radio de una singularidad, Karl Schwarzschild (Alemania 1873-1916) encontró una solución para la ecuación anterior y pudo, por tanto, describir la geometría del espacio-tiempo. Es decir, pudo describir cómo se deformaría el espacio-tiempo en presencia de un objeto de densidades muy elevadas.
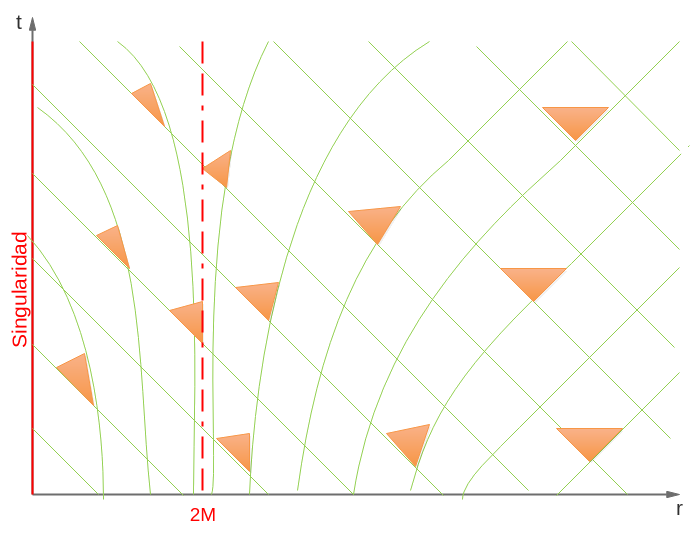
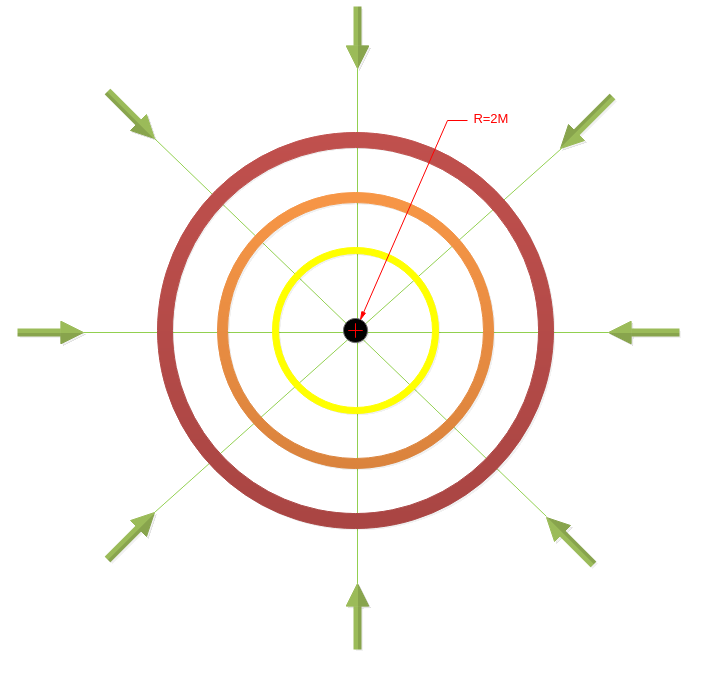
La singularidad está en r=0 y perdura en el tiempo. Observamos que lejos de ella, el espacio-tiempo no está deformado, y nuestros conos de luz se encuentran como siempre, enfocados hacia arriba. Sin embargo, conforme nos acercamos a la singularidad, las líneas que describen la forma del espacio-tiempo se van deformando, se van curvando, y los conos de luz quedan cada vez más inclinados hacia ella.
Esto quiere decir que conforme más nos acercamos a la singularidad, más enfocado está nuestro futuro hacia ella y menos probabilidades tendremos de avanzar hacia un futuro que la esquive.
Schwarzschild encontró que hay un punto de ‘no retorno’, llamado radio de Schwarzschild, que será igual a dos veces la masa de la singularidad. Una vez cruzamos esa frontera, el espacio-tiempo está tan deformado que nuestro cono de luz apunta completamente a la singularidad.
La singularidad es inevitable, se encuentra irrevocablemente en nuestro futuro
¿Qué quiere decir ésto? Viajemos en nuestra nave espacial en dirección al agujero negro y vayamos emitiendo pulsos de luz. Conforme nos acercamos, a nuestros pulsos de luz cada vez les cuesta más trabajo salir en dirección contraria al agujero negro. Una vez que cruzamos el radio de Schwarzschild ningún pulso de luz podrá salir. Recordemos que la velocidad de la luz es una velocidad límite, que no podíamos salirnos de nuestro cono de luz. Si la luz no puede escapar a la singularidad, nada puede hacerlo, porque nada puede viajar más rápido que la luz.
Si no puede salir nada, a un observador que esté fuera de la singularidad no le llegará nada, ningún tipo de señal que pueda ver o medir. Es decir, para quien esté fuera de la singularidad, lo único que verá será un hueco negro, un agujero negro.
Si os estáis preguntando a donde va la masa de esa enorme estrella que se comprime, o toda la masa y la energía que cae dentro del agujero negro, qué es lo que pasa dentro, no podemos responderte. Por la misma razón por la cual al principio de este post no podíamos saber cómo era nuestra función en x=0, justo en el agujero negro no podemos saber qué pasa, porque nuestras ecuaciones no se pueden resolver.
Un agujero negro es una singularidad en el espacio de Minkowski
El 10 de Abril de 2019 se obtuvo por primera vez una imagen real de un agujero negro situado en la galaxia M87.

El anillo brillante es materia y luz que orbita el agujero negro y va cayendo en él. El radio del hueco negro que vemos en el centro se corresponde con el radio de Schawarzschild. El borde de ese hueco negro, justo la última línea en la que se puede percibir alguna señal, se llama horizonte de sucesos.
Einstein se equivocaba cuando decía que «Dios no juega a los dados con el universo». Considerando las hipótesis de los agujeros negros, Dios no sólo juega a los dados con el universo: a veces los arroja donde no podemos verlos.
Stephen Hawking


Hola Tatiana, estupenda entrada. Una pregunta, cuando pones que si hacemos un cambio de coordenadas y pasamos a cartesianas, ya podemos calcular el potencial en el punto r=0, ¿realmente es posible? Yo creo que te sigue dando el denominador 0, con lo que no hay manera posible de calcularlo. Bueno, sí es posible. Da +infinito. Que es un número como otro cualquiera, sin ningún otro particular. Un saludo