A menudo cuando estudiamos matemáticas, el pensamiento que nos viene más de una vez a la cabeza es ‘¿Y ésto para qué?’. Como las matemáticas son el lenguaje de la física, hoy vamos a coger un concepto matemático y lo llevaremos hasta sus últimas consecuencias físicas: el concepto de derivada.
Empezaremos por lo básico. Igual que la suma es una operación que se le aplica a, por ejemplo, dos números, la derivada es una operación que se le aplica a las funciones.
Una función es una expresión matemática que nos relaciona objetos. Por ejemplo: en la expresión y=x+1 cuando x=1 nos relaciona el objeto x=1 con el objeto y=2 (basta con sustituir en la expresión la x por 1 y hacer la operación indicada, en éste caso y=1+1=2). Y así con todos los valores que queramos darle a la x. Así pues, y es lo que llamamos una función, en la que su variable independiente es la x, ya que su valor lo damos nosotros, no depende de nada; y su variable dependiente es la y, ya que su valor depende del valor que le hayamos dado a la x. Puesto que y depende del valor de x, también podemos escribir como f(x) y la función nos quedaría f(x)=x+1
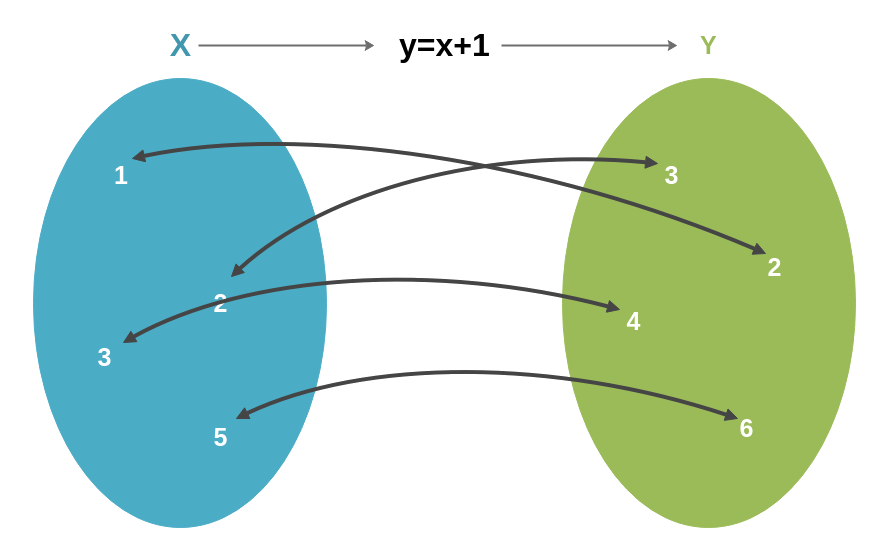
También podemos despejar y tener x=y-1, de manera que ahora y es la variable dependiente, x la independiente, nos quedaría f(y)=y-1, pero seguimos relacionando los mismos elementos.
Las ecuaciones que nos enseñaban en el instituto en física son, al fin y al cabo, funciones que nos relacionan magnitudes que observamos o medimos (serán nuestras variables independientes) con otras que no podemos medir directamente (que serán nuestras variables dependientes), mediante las expresiones correspondientes
Si nos vamos a los libros, veremos que la definición matemática de lo que es una derivada nos viene dado con una cosa tan abstracta como ésto
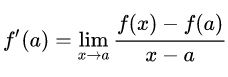
Traduciéndolo, viene a decir algo así como que la derivada de una función en un punto a es lo que vale la función en cualquier punto x menos lo que vale la función en el punto a, dividido entre la distancia de cualquier punto al punto a y todo ello llevado al caso límite en el que cualquier punto x es muy muy proximo al punto a, sin llegar a serlo.
¡¿Ein?!
No entremos en pánico todavía, porque todo ésto puede expresarse en lenguaje coloquial como
La derivada de una función es la expresión que nos dice cómo cambia esa función conforme hacemos pequeños cambios en una de sus variables
Para ver qué aplicaciones tiene el concepto de derivada, nos ayudarán Pepe y María: María sale de su casa a las 20.30h en coche. Ha quedado en recoger a Pepe en la suya, que está a 4km de la de María, para ir al cine a ver una película que empieza a las 21.00h. El cine está a 7km de la casa de Pepe. Es decir, María, que está a las 20.30h en su casa, tiene que llegar al cine a las 21.00h, y para pasar de un lugar a otro habiendo recogido a Pepe tiene que recorrer 11km.
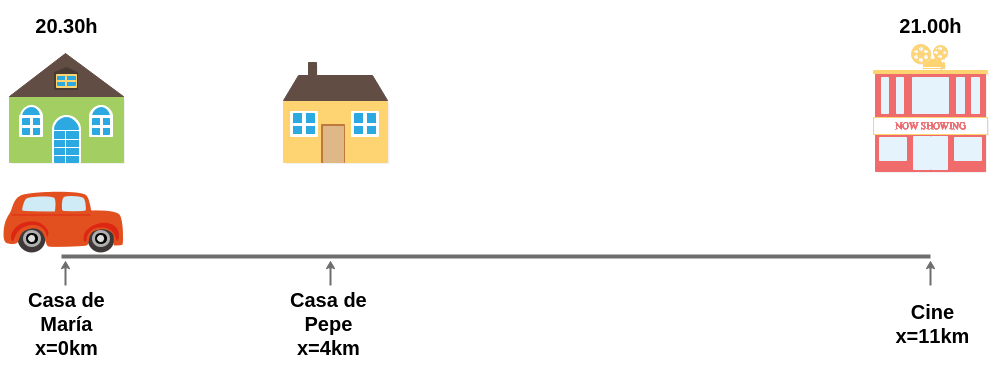
Tendremos una función que nos da la posición de María con respecto al tiempo t: x(t). Gracias a esta función, podremos saber donde está María en cada momento. Por ejemplo, sabemos que a las 20.30h María estará en la posición que corresponde a su casa. Pero, ¿qué pasa cuando María empieza a moverse? Cuando avanzamos en el tiempo, María comienza su camino hacia la casa de Pepe, cambiando su posición en cada instante.
Para conocer cuánto cambia de posición María, nos basta con x(t): en t=20.30h su posición será x=0 y que en t=21.00h su posición será x=11 (estará en el cine). Restando las dos posiciones sabemos que María se ha movido 11km.
Para saber cómo se ha movido María necesitamos conocer no sólo cuánto cambia x(t), sino también cómo lo hace. Si recordamos lo que hemos dicho antes, la derivada es lo que nos permite conocer cómo cambia la función x(t) conforme hacemos pequeños cambios.
Así pues, lo que necesitamos es la derivada de nuestra función posición, que matemáticamente se expresa así
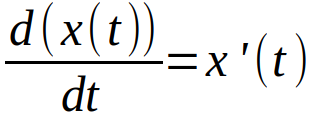
La derivada de la función posición conforme hacemos pequeños cambios en el tiempo, conforme avanza el tiempo, es lo que comúnmente conocemos como velocidad v(t).
El significado físico de derivar una vez la función posición con respecto al tiempo es la velocidad
Con los datos del ejemplo, a una velocidad constante de 20km/h María tardará 12 minutos en llegar a casa de Pepe, es decir a las 20.42h. María le avisa y Pepe le dice que enseguida baja pero en realidad está metiéndose en la ducha. Hasta las 20.55h Pepe no se monta en el coche y María arranca hasta volverse a poner a una velocidad constante de 20km/h, pero hace cuentas y deduce que si hace el resto del trayecto a esa velocidad no llegarán a tiempo a la película. ¿Qué debe hacer para llegar? Ir más rápido, es decir, modificar su velocidad. Esto ya nos suena.
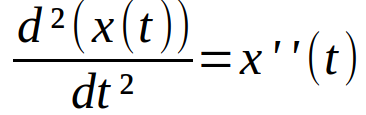
Al igual que antes con la posición, si ahora queremos saber cómo tiene que modificar su velocidad tendremos que derivar la velocidad. La derivada de la velocidad nos dará cómo cambia ésta conforme hacemos pequeños cambios en el tiempo, y a ésto comúnmente se le llama aceleración a(t).
El significado físico de derivar dos veces la posición con respecto al tiempo es la aceleración.
Y ahora que sabemos qué son exactamente la velocidad y la aceleración, vamos a llevarlo hasta las últimas consecuencias.
Para la siguiente vez que quedan para ir al cine, María sigue enfadada por la tardanza de Pepe, así que esta vez deciden ir cada uno en su coche: Ambos salen de su casa a la misma hora, pero María se mueve a una velocidad constante de 20km/h y Pepe lo hace a 30km/h. Es decir, Pepe se mueve a 10km/h respecto de María. Y ambos ven una moto.
Si echamos una foto, es decir, paramos el tiempo, veremos ésto
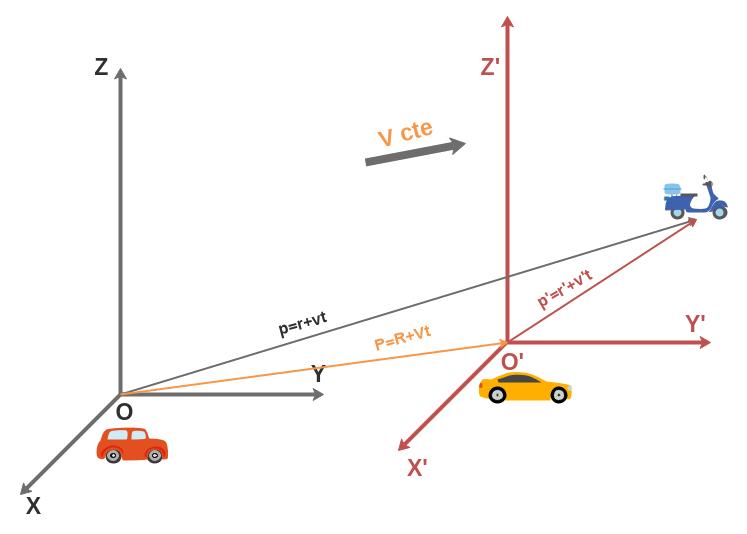
Hay dos maneras de definir pues la posición de la moto respecto a María (O):
- Midiendo directamente la posición desde María hasta la moto (gris): p=r+vt
- Midiendo la posición desde María hasta Pepe y luego desde Pepe hasta la moto y sumarlos: (naranja+rojo): p=P+p’, es decir p=R+Vt+r’+v’t
Pero en lo que todos estaremos de acuerdo es en que, lo midas como lo midas, la posición de la moto respecto a María es la que es, con lo cual ambas maneras de hacerlo tienen que dar el mismo resultado. Ésto significa que podemos igualar ambas formas:
r+vt=R+Vt+r’+v’t
Y ahora vamos a seguir aplicando el concepto estrella de hoy: vamos a derivar esta ecuación posición respecto del tiempo. Para ello tendremos en cuenta que:
- r, R y r’ son posiciones iniciales, es decir, donde estaban María, Pepe y a moto antes de que el tiempo empezase a discurrir, por lo tanto no dependen del tiempo, así que su derivada será 0
- La derivada de vt será v (y así con Vt y v’t)
Por lo tanto nos quedará:
v=V+v’
Eso significa que María no verá la misma velocidad de la moto si la mide por un camino o por otro.
Bueno, vamos a derivar otra vez. Ahora derivamos la ecuación velocidad respecto del tiempo, a ésto le habíamos llamado antes aceleración y lo definíamos como pequeños cambios en la velocidad. Pero como habíamos dicho que Pepe se mueve a una velocidad constante respecto a María, esa velocidad (que hemos llamado V), no sufrirá cambios. Si no cambia, su derivada será cero, así que nos queda:
a=a’
Eso significa que María, mida por el camino que mida la aceleración, la verá igual
La velocidades dependen de cómo se midan, son relativas; mientras que las aceleraciones no depende de cómo se mida, son absolutas.
Lo que hemos hecho es desplazar el sistema de referencia de Pepe paralelamente al del María y a velocidad constante. Este tipo de desplazamientos de llaman Transformaciones de Galilei y junto con las rotaciones y las traslaciones espaciales o temporales conforman el grupo de simetría de la mecánica newtoniana, que se llama Grupo de Galilei. Es una demostración de cómo la física y las matemáticas se entrelazan: a base de experimentación y de expresar los resultados matemáticamente de forma rigurosa puedes terminar descubriendo simetrías matemáticas subyacentes que le dan sentido a la física y te confirman que vas por buen camino.
Comentarios