A la hora de hablar de Relatividad, se necesita un apellido. Y es que Einstein construyó primero lo que llamamos Relatividad Especial (1905) y luego necesitó unos cuantos años en clase de mates para pulir lo que llamó Relatividad General (1915-1916). Hablemos hoy de la primera de ellas. Empecemos recordando algunos conceptos:
- Observador inercial: según Newton, es aquel que puede explicar el movimiento sin considerar fuerzas ficticias, como la fuerza centrífuga. En otras palabras, es el observador que consideramos que está en reposo respecto a lo que estamos observando.
- Observador no-inercial: es aquel que necesita de fuerzas ficticias para explicar el movimiento. Es decir, es aquel que se mueve con el sistema y por tanto no puede ver determinadas fuerzas que afectan al sistema, ya que también las está sufriendo, y para explicar el movimiento necesita introducir fuerzas ficticias.
Hablemos de Pepe y María:Supongamos que Pepe está asomado en la proa de uno de esos barcos enormes que se deslizan por un mar en calma sin que se note. Su amiga María esta en el puerto. La pregunta es: ¿Quien se aburre esperando a su amigo y quien está impaciente por llegar? O en otras palabras, ¿quién es el observador inercial y quien el no-inercial?
Bueno, Newton lo tendría claro: María es la que está en reposo y por tanto es inercial y Pepe es el que se mueve y por tanto el no-inercial. En otras palabras, María se aburre esperando y Pepe está deseando llegar. Esa es la primera intuición para el 99% de la población, acostumbrados a vivir en un mundo newtoniano.
Pero es que habíamos dicho que Pepe viajaba en un gran barco en un día de mar calmado. Además, aún no se ve la costa, así que Pepe no tiene puntos de referencia y no sabe si el barco está quieto o efectivamente va camino de ver a María. No hay ningún experimento físico que ambos puedan hacer que les den resultados diferentes y por tanto no tienen forma de saber quien es quien. En efecto, María podrá tirar hacia arriba una pelota y le volverá a caer en la mano, pero es que si Pepe hace el mismo experimento, también le caerá en la mano. Y aunque lo primero nos resulta trivial, lo segundo ha dado lugar a algún que otro quebradero de cabeza.
Fue Galileo quien se atrevió a dar forma a este pensamiento y formuló el primer principio en el que se basa la Relatividad Especial
Principio de Relatividad (Galileo-1600): es imposible determinar mediante experimentos mecánicos si un observador esta en reposo o en movimiento rectilíneo uniforme.
Entonces, volviendo a la pregunta de antes, tenemos que Pepe puede pensar ‘oye, soy yo quien está esperando a María y ella es la que viene hacia mi’. Galileo le da todo el derecho a opinar que es él quien está en reposo y es la costa (y por tanto María) quien se mueve hacia él, de manera que desde su punto de vista Pepe es inercial y María es no-inercial.
¿Quien lleva razón? Pues… Ambos. Ya que son indistinguibles, podemos elegir tanto a uno como a otro como nuestro observador inercial. Así, podemos reformular
1|Principio de Relatividad: todos los observadores inerciales son equivalentes, es decir, todos ven la misma física.
Ya tenemos el primer principio de la Relatividad Especial. El segundo principio proviene de una serie de hechos experimentales y por el hecho de que si se asume que todas las leyes de la física son iguales para todos los observadores, la velocidad de la luz debe ser constante.
2| Velocidad constante de la luz: La velocidad de la luz en el vacío (unos 300.000km/s) es igual para todos los observadores, independientemente del movimiento de la fuente.
Con estos dos principios hemos construido toda la Relatividad Especial, que llevó a Einstein a indagar un poco más hasta darse cuenta de que la Especial era sólo un caso límite de la Relatividad General, que una vez formalizada se convirtió en la mayor revolución de la física desde Newton. Desde el buen funcionamiento de los GPS hasta la forma del universo, todo ello son ganancias que nos proporcionó Einstein.
Pero, ¿a qué precio? ¿Qué concesiones tuvo que hacer el paradigma del pensamiento científico para poder jugar con estos juguetes nuevos? El coste fue la intuición.

Y es que, si aceptamos que la velocidad de la luz es constante, empiezan a pasar cosas raras.
Imaginemos ahora que el barco donde va Pepe se desliza de forma igualmente imperceptible para él, pero a velocidades cercanas a las de la luz. E imaginemos que tiene lo que se llama un reloj de luz, que no es más que un pulso de luz que rebota entre un espejo en el suelo del barco y el techo. Como conocemos el espacio que hay entre ambos espejos (s) y la velocidad de la luz (c), podemos calcular el tiempo que tarda la luz en llegar de un espejo a otro (t).
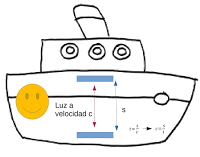
Pero lo que ve María, desde fuera del barco, es muy diferente: como el barco va a casi la velocidad de la luz, ella ve al barco desplazarse en lo que tarda el pulso de luz en subir y bajar.
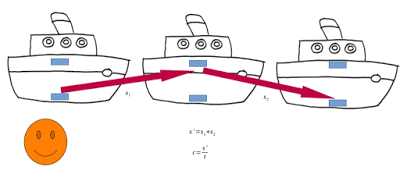
Como nuestro segundo principio de la Relatividad Especial nos dice que en ambos casos la velocidad de la luz c es la misma, tenemos:
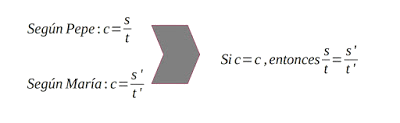
Se puede ver en los dibujos claramente que el espacio que recorre la luz según Pepe es menor que el espacio que recorre la luz según María, de manera que para que ésto se cumpla, el tiempo que mide María también debe ser mayor que el tiempo que mide Pepe.
Éste es el primer peaje que la Relatividad Especial nos hace pagar: El tiempo no es igual para todos los observadores
Pero la cosa no termina ahí, porque ya que a Pepe le va el reloj más lento que a María, si ambos se ponen a medir cuánto tiempo tarda el barco en recorrer la ensenada, tampoco se pondrán de acuerdo: para María el barco será más corto que para Pepe, o lo que es lo mismo, Pepe ve la ensenada contraída respecto a como lo ve María. (Si Pepe ve el barco más largo, es que la ensenada le parece más corta).
Éste es el segundo peaje que la Relatividad Especial nos hace pagar: La longitud de los objetos en movimiento no son iguales para todos los observadores.
La plasticidad del espacio y el tiempo es un concepto contraintuitivo y difícil de asimilar en todo su alcance, pero la verdad es que la Relatividad ha pasado los exámenes con nota, con respaldos empíricos de los que hablaremos otro día.
Ejemplo de los Muones
Los muones son partículas que se crean en la zona alta de la atmósfera, a unos 10000m de la superficie. Si le preguntamos al muón cuánto tiempo vive nos dirá que unos 2,2 microsegundos. Además, tienen la particularidad de que van casi a la velocidad de la luz (0.99c). Si hacemos la cuenta y multiplicamos el tiempo que viven por la velocidad a la que van, veremos que debería darles tiempo a recorrer únicamente algo más de 600m.
Bien, entonces si salimos a buscar muones dando un paseo por la superficie terrestre no deberíamos poder encontrar ninguno, ya que mueren (se desintegran) a 9400m del suelo. Eso fue lo que hiceron en 1963 David Frisch y James Smith, pero para su sorpresa midieron nada más y nada menos que 412 muones por hora a nivel del mar. ¿Cómo es ésto posible?
Veamos qué es lo que mido desde la superficie, como María: mi reloj va más rápido, es decir, el muón vive más tiempo desde mi punto de vista. Tras realizar las correspondientes correcciones, veo que vive unos 34,8 microsegundos. Haciendo lo mismo de antes, vemos que en este tiempo el muón recorre a la velocidad de la luz 10419m y por eso le da tiempo llegar a la superficie.
Pero vamos ahora a montarnos encima del muón, como Pepe: según su reloj, vive 2,2 microsegundos, pero nuestro espacio ahora se contrae de manera que la distancia desde donde se crea el muón hasta la superficie tras aplicar las correcciones es sólo de unos 600m, con lo que le da tiempo de sobra a llegar.
La maleabilidad del espacio y el tiempo no parece un precio demasiado alto por una viaje en muón, ¿no?

Comentarios